Рассчитать объем песка для разных строительных целей
Нужный объем песка постоянно рассчитывают строители при выполнении широкого спектра работ:
- засыпки и поднятия участков;
- строительстве фундаментов и заборов;
- формировании стяжки;
- заливке отмостки;
- приготовлении бетона;
- благоустройстве территорий.
Точный расчет необходимого объема песка экономит время и деньги
В большинстве случаев для строительных целей используют карьерный или речной песок. Удельный вес 1 м³ карьерного песка – 1 500 кг, речного – 1 630 кг.
Речной песок более тяжелый, что объясняется меньшим размером зерен и большей плотностью материала. Приобретать песок рекомендуется в сухую погоду, когда в нем содержится минимум избыточной влаги.
Расчет объема песка для засыпки
Предположим, нам нужно засыпать участок площадью 6 соток (600 м²), подняв его на уровень 0,5 м.
Для определения объема песка следует умножить площадь участка на высоту засыпки.
После засыпки песок уляжется, на это нужно сделать поправку. Коэффициент уплотнения колеблется в пределах 1,05–1,3, в зависимости от вида песка. Для нашего примера возьмем среднюю величину 1,1, то есть добавим к рассчитанному объему еще 10 %. В результате получим 300 х 1,1 = 330 м³ песка.
Песок доставляют на самосвалах с разным объемом кузова
Заказывая материал, нужно обязательно уточнить, каким транспортом его доставят. В кузов КамАза, к примеру, помещается 12 м³ песка, МАЗа – 6 м³, ЗИЛа – 3 м³. При загрузке с горкой объем может увеличиться до 1,5 раза.
Расчет объема песка для бетонной смеси
При расчете количества песка для строительной смеси при создании фундаментов или стяжки нужно учитывать марку цемента.
Из-за неправильного объема песка снизится качество бетона
Сначала вычисляют необходимый объем бетона по формуле, приведенной выше. Исходя из класса бетона определяют требуемое количество песка.
Рассчитать его можно двумя способами:
- По долевому соотношению песка и цемента
Для разных марок цемента используют разные пропорции. Показатель включения песка варьируется от 2–4,5 : 1.
Предположим, мы используем цемент марки М-200, для которого принято соотношение 2,8 : 1. Значит, на 100 кг цемента нужно взять 280 кг песка.
- По процентному содержанию в бетоне
Зная необходимый объем бетона, просчитываем объем песка, исходя из его процентного содержания в смеси. В зависимости от класса бетона доля песка колеблется в пределах 29–36 %. Значит, нам потребуется минимум 29 м³ песка.
Расчет объема песка в конусной насыпи
Представим ситуацию, когда песок уже выгружен из самосвала и точно неизвестно, сколько его было в каждой машине. Просчитать объем конусной насыпи простым сложением не получится.
Для расчета объема песка в конусной насыпи нужно замерить ее радиус и высоту
Узнать точный объем песка в конусной насыпи можно по формуле: V = ⅓π х R² х H, где R – радиус конуса, H – его высота, π = 3,14.
Предположим, высота насыпи 1 метр, а радиус – 1,5 м. Рассчитываем:
Конечно, песок не дает идеального конуса, но примерно оценить объем таким образом возможно. А зная точный объем необходимого и имеющегося в наличии песка, проще планировать расход и поставки. Не будет простоев в работе, жесткой экономии, вынужденного снижения качества бетона и, соответственно, прочности готовых конструкций.
Коэффициент разрыхления грунтов – что это и как его рассчитать
Коэффициент первоначального разрыхления грунтов, а также показатели плотности приведены по категориям в таблице.
| Наименование грунта | Категория грунта | Плотность грунта тонн/м3 | Коэффициент разрыхления грунта |
| Песок рыхлый, сухой | I | 1,2…1,6 | 1,05…1,15 |
| Песок влажный, супесь, суглинок разрыхленный | I | 1,4…1,7 | 1,1…1,25 |
| Суглинок, средний и мелкий гравий, легкая глина | II | 1,5…1,8 | 1,2. -1,27 -1,27 |
| Глина, плотный суглинок | III | 1,6…1,9 | 1.2…1.35 |
| Тяжелая глина, сланцы, суглинок с щебнем, гравием, легкий скальный грунт | IV | 1,9…2,0 | 1,35…1,5 |
К основным свойствам грунтов, влияющим на технологию и трудоемкость их разработки, относятся плотность, влажность, разрыхляемость.
Основными свойствами грунтов, влияющими на трудоёмкость их разработки и технологии, являются влажность, разрыхляемость и плотность.
Влажность грунта – это степень насыщения его водой. Её определяют как отношение массы воды в самом грунте к массе его твёрдых частиц. Выражается влажность в процентах. При влажности менее 5% грунты считаются сухими, при более чем 30% — мокрыми. Трудоёмкость разработки грунта повышается с увеличением его влажности. Но исключением является только глина: сухую её разрабатывать сложнее. Но при порядочной влажности глинистые грунты обретают липкость, что значительно усложняет их разработку.
Плотность – это масса одного кубического метра грунта в плотном теле (естественном состоянии). Несцементированные грунты обладают плотностью от 1,2 до 2,1 тонн/м3, скальные – до 3,3 тонн/м3.
Цены на разработку грунта за 1м3 механизированным способом
Оставьте заявку
При разработке грунт разрыхляется, увеличиваясь при этом в объёме. Именно данное количество грунта и транспортируется самосвалами к месту утилизации или складирования. Это явление называется первоначальным разрыхлением грунта, при этом характеризуясь коэффициентом первоначального рыхления (Кр), представляющего собой отношение объёма уже разрыхленного грунта к его объёму в естественном состоянии.В насыпи разрыхлённый грунт уплотняется воздействием массы вышележащих грунтов или с помощью механического уплотнения, смачивания дождём, движения транспорта и т. д. Только грунт не занимает объёма, занимавшего до разработки длительное время. Он сохраняет остаточное разрыхление, которое измеряется коэффициентом остаточного разрыхления (Кор).
Из вышеизложенного следует, что, рассчитывая общую стоимость выполнения работ, необходимо знать геометрические размеры будущего котлована. При этом коэффициент первоначального разрыхления нужно умножить на объём грунта в будущем карьере. Именно это количество грунта будет разработано и вывезено со строительного объекта для складирования или утилизации. И именно эта цифра умножается на цену разработки, погрузки и транспортировки одного кубического метра грунта.
Рассчитать объем щебня по площади: таблицы и формулы
В этой статье подробно описано, как рассчитать объем щебня по площади. Чтобы вычислить его, нужно перемножить насыпную плотность нерудного материала, длину и ширину участка, который предстоит засыпать, а также толщину щебневого слоя.
Важные характеристики щебня
Насыпная плотность – масса 1 куб. м щебня в неуплотненном состоянии. Она указана в сертификате соответствия и различна для разных фракций и видов материала. Например, известняк — самый легкий из-за слоистой и пористой структуры, а гранит — наиболее тяжелый ввиду высокой плотности. Если нет возможности ознакомиться с сертификатами, ориентируйтесь на примерные показатели в соответствии с ГОСТ 8267-93, ГОСТ 8269.0-97.
Например, известняк — самый легкий из-за слоистой и пористой структуры, а гранит — наиболее тяжелый ввиду высокой плотности. Если нет возможности ознакомиться с сертификатами, ориентируйтесь на примерные показатели в соответствии с ГОСТ 8267-93, ГОСТ 8269.0-97.
Таблица 1. Насыпная плотность щебня разных видов
| Щебень | Размер фракции,мм | Насыпная плотность,кг/м3 |
|---|---|---|
| Гранитный | 20 – 40 | 1370 – 1470 |
| 40 – 70 | 1380 – 1450 | |
| 70 – 250 | 1400 | |
| Известняковый | 1250 | |
| 20 – 40 | 1280 | |
| 40 – 70 | 1330 | |
| Гравийный | 0 – 5 | 1600 |
| 5 – 20 | 1430 | |
| 20 – 40 | 1400 | |
| 40 – 100 | 1650 | |
| >160 | 1730 | |
| Шлаковый | независимо от размера частиц | 800 |
Перед тем как рассчитать, сколько нужно щебня на площадь, проанализируйте сопутствующие факторы. Основной из них – коэффициент уплотнения. Эта безразмерная величина характеризует, насколько объем материала уменьшится при трамбовке катком или в ходе естественного уплотнения при перевозке. ГОСТ 8267-93 не требует обязательного указания этого параметра в сопроводительных документах, поэтому ориентируйтесь на условия СНиП 3.06.03-85:
Основной из них – коэффициент уплотнения. Эта безразмерная величина характеризует, насколько объем материала уменьшится при трамбовке катком или в ходе естественного уплотнения при перевозке. ГОСТ 8267-93 не требует обязательного указания этого параметра в сопроводительных документах, поэтому ориентируйтесь на условия СНиП 3.06.03-85:
- при транспортировке в грузовой машине коэффициент равен 1,1;
- при трамбовке высокопрочных марок гранитной, гравийной щебенки– около 1,3;
- при утрамбовке материалов марок 300 – 600 – до 1,52.
Показатель актуален для насыпных материалов с размером фракций 40 – 70 и 70 – 120 мм. Для других видов его обычно не применяют, поскольку в дорожно-строительных работах мелкую щебенку используют для расклинцовки (заполнения пустот), а не для обустройства оснований. Однако из нее делают фундаментную подушку, а для этих целей подходит щебенка 20 – 40 мм. Если нужно произвести расчет щебня для фундамента, также применяйте коэффициент 1,3.
Пример расчета для фундамента
Рассчитать щебень на фундамент предельно просто. В первую очередь вычисляют объем щебневой подушки по формуле:
V= Sh= abh, где:
S – площадь, а h – высота,
a – длина, b – ширина, h – высота.
Поскольку мы рассчитываем объем щебня по площади, она нам уже известна. Ее следует умножить на толщину подушки (рекомендованное значение – от 20 до 30 см). Если размеры монолитного фундамента равны 6х10 м, а толщина щебеночного слоя – 25 см, рассчитаем объем:
6 х 10 х 0,25 = 15 куб. м
Для фундаментной подушки традиционно используют нерудные материалы с показателями морозостойкости не менее F300, прочные и стойкие к воздействию влаги. Обычно это гранит или гравий. Но первый существенно дороже, а также обладает природной радиоактивностью, поэтому строить жилые дома с его применением следует очень осторожно (например, нельзя использовать его при возведении стен, перекрытий).
Насыпная плотность гравийного щебня 20 – 40 мм – около 1400 кг/куб. м, а коэффициент уплотнения в данном случае – 1,3. Зная эти параметры, произведем несложный расчет:
1,4 т х 15 куб. м х 1,3 = 27,3 т.
Мы получили общий вес нерудных материалов для засыпки 60 кв. м площади слоем в 25 см. Чтобы рассчитать необходимый объем, делим полученную величину на насыпную плотность материала:
27,3 т : 1,4 т/куб. м. = 19,5 куб. м
Расчет щебня на дорогу
Пользуясь приведенными формулами, несложно понять, как рассчитать количество щебня на дорогу. Просто подставьте необходимые значения:
V = S пл.покрытия х h толщина слоя
Полученный объем перемножьте с насыпной плотностью щебенки (обычно используют гранитную 70 – 120 мм) и коэффициентом 1,3 по формуле:
m = V х уд. плотность х коэфф. уплотнения
Затем разделите массу на удельную плотность и получите объем щебня, который нужно приобрести для проведения строительных работ.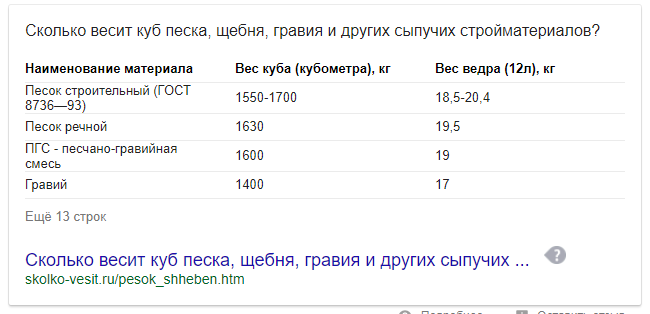
Доставка нерудных материалов по ЦФО
Позвоните нам!
или оставьте заявку
Подсчет песчинок | Фред Хейнс
Вы когда-нибудь задумывались, сколько песчинок на пляже? Или, может быть, более простой вопрос о том, сколько песчинок помещается в 20-миллилитровую пробирку для сбора, похожую на ту, что на фото на обложке? Я полагаю, что вы, вероятно, нет, но я сделал.
Для начала мы знаем, что 20 мл равны 20 кубическим сантиметрам. Теперь также сделаем три предположения:
- предполагают среднезернистый, хорошо отсортированный песок с диаметром зерен 0.33 мм (все зерна одинаковые)
- предполагают хорошо округлые сферические зерна
- предполагает гексагональную плотную упаковку (HCP) зерен, при которой чередующиеся слои зерен располагаются друг над другом. Каждая сфера будет касаться 12 других, 6 в пределах своего слоя и 3 в слоях выше и ниже. При такой упаковке зерен зерна будут составлять 60% объема флакона.
 Остальное будет поровым пространством. Иными словами, пористость песка будет 40% .
Остальное будет поровым пространством. Иными словами, пористость песка будет 40% .
Теперь мы готовы заняться математикой.Есть несколько способов выполнить этот расчет, но давайте поработаем двумя разными способами. Почему, спросите вы, мы делаем это двумя способами? Ну, потому что мы можем. И потому что математика с целью — это весело!
Первый метод : Преобразуйте задачу в стандартный куб и работайте только с размерами длины. Этот простой метод требует только первых двух предположений.
- Каждое ребро куба объемом 20 кубических сантиметров будет иметь длину 2,714 см. (или кубический корень из 20). Да, я знаю, что нарушил правила значащих цифр при этом преобразовании и других).
- Позволяет выровнять 82,2 куба диаметром 0,33 мм по каждому краю (27,14 мм/0,33 мм = 82,2)
- 2 x 82,2 x 82,2 составляет ~555 000
- В объеме 20 кубических сантиметров или 20 мл содержится около 555 000 крошечных кубиков с длиной ребра 0,33 мм.
 Каждый из них мог бы вместить одно сферическое зерно, если бы они были сложены друг над другом.
Каждый из них мог бы вместить одно сферическое зерно, если бы они были сложены друг над другом.
Конечно, они бы никогда так не сложились, так что…
Второй метод : Постройте задачу для учета сферической формы зерна, которая больше соответствует реальному песку и включает третье предположение.
- Объем сферы равен 4/3 r 3 , где π равно 3,1416, а r — радиус сферы (в данном случае 0,166 мм). Таким образом, объем одной песчинки составляет 0,192 кубических миллиметра.
- В 20 кубических сантиметрах (или мл) содержится 20 000 кубических миллиметров.
- Таким образом, в этом объеме (20 000/0,0192) есть место для примерно 1 040 000 песчинок.
- НО подождите, мы взяли HCP для этих зерен и пористость 40%. Следовательно, мы должны умножить наше рассчитанное количество зерен на процент объема, который будет занят зернами.(60% от 1 040 000 = 624 000,
Большее число (624 000 зерен в объеме 20 мл), вероятно, является более точной оценкой, поскольку оно включает в себя концепцию, согласно которой зерна будут заполнять пространство более эффективно, чем просто располагаясь по центру нижнего. В действительности все зерна не имеют одинакового размера или формы, и эти вариации размеров обычно обеспечивают более плотную упаковку, поскольку более мелкие зерна располагаются в промежутках между более крупными зернами. Однако я не думаю, что планирую подсчитывать песчинки в каких-либо из моих 20-миллилитровых пробирок для проб, чтобы убедиться в этом.
В действительности все зерна не имеют одинакового размера или формы, и эти вариации размеров обычно обеспечивают более плотную упаковку, поскольку более мелкие зерна располагаются в промежутках между более крупными зернами. Однако я не думаю, что планирую подсчитывать песчинки в каких-либо из моих 20-миллилитровых пробирок для проб, чтобы убедиться в этом.
Флакон объемом 20 мл со среднезернистым песком, богатым гранатом, с пляжа Хэмлин на озере Онтарио. Только представьте, более полумиллиона песчинок!
Помните, что размер зерен песка варьируется от 0,06 мм (очень мелкий) до 2,0 мм (очень крупный). Количество песчинок в 20-миллилитровой пробирке для образца будет сильно различаться в зависимости от размера песчинок. Я позволю вам вычислить эту разницу. Любой, кто это сделает, может сообщить о своих результатах на следующем собрании клуба.
Я также предоставлю вам возможность посчитать, сколько 20-миллилитровых флаконов потребуется, чтобы убрать весь песок с вашего любимого пляжа!
Кто сказал, что математика бесполезна?
Насколько велик миллиард песчинок? – СидмартинБио
Насколько велик миллиард песчинок?
Если представить себе куб шириной 1 фут в каждом направлении, он содержит около миллиарда песчинок, которые будут весить от 50 до 100 фунтов, в зависимости от того, насколько влажный песок. Когда мы посчитаем, вы увидите, что большие замки из песка складываются быстро.
Когда мы посчитаем, вы увидите, что большие замки из песка складываются быстро.
Сколько песчинок в унции?
Преобразование унций в зерна
| унций | 1 | 1000 |
|---|---|---|
| зерно | 437,5 | 437500 |
Сколько стоит триллион песчинок?
Отсчитай 1000 песчинок, затем разбросай еще 999 000 – твоя догадка! – просто убедитесь, что у вас есть компактный мешочек песка в 1000 зерен на стороне.Это 10 в 6-м, а триллион — 10 в 12-м.
Сколько песчинок в среднем на пляже?
Я буду следовать оценкам и расчетам, сделанным доктором Джейсоном Маршаллом, также известным как Математический Чувак. По словам Джейсона, на Земле около 700 триллионов кубометров песчаных пляжей, что соответствует примерно 5 секстиллионам песчинок.
Сколько весит 1 миллиард рисовых зерен?
15 625 кг
Вес 1 миллиарда зерен = 15 625 кг, 34447 фунтов, 15.63 тонны, 17,22 тонны США.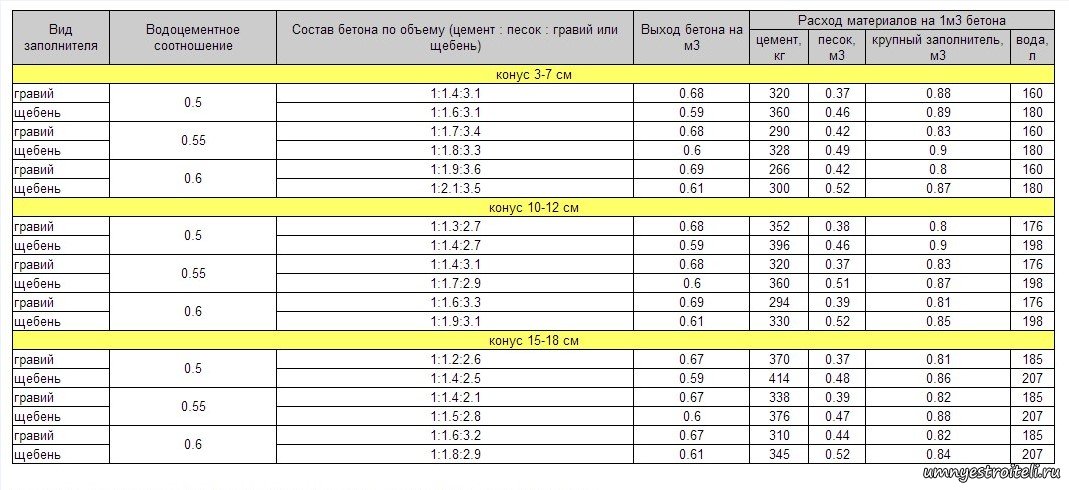 Предположим: плотность: 1,22 л/кг.
Предположим: плотность: 1,22 л/кг.
Как называется число с 14 нулями?
Числа больше триллиона
| Имя | Количество нулей | Группы из (3) нулей |
|---|---|---|
| Ундециллион | 36 | 12 |
| Дуодециллион | 39 | 13 |
| Тредециллион | 42 | 14 |
| Кватттуор-дециллион | 45 | 15 |
Сколько весит 1 песчинка?
0.0044 грамма
При огромном разнообразии размеров зерен и составных материалов песчинки весят в среднем 0,0044 грамма.
Сколько гран составляет слизняк весом 58 унций?
Итак, 0,625 унции в гранах = 0,625 умножить на 0,0000647989 = 273,437542198 гран, точно.
Сколько весит весь песок в мире?
Вес любого количества песка зависит от того, сколько в нем воды. Подсчитано, что сухой песок весит примерно 100 фунтов (45 кг) на кубический фут. Влажный песок, естественно, тяжелее и весит от 120 до 130 фунтов (от 54 до 58 кг) на кубический фут.
Влажный песок, естественно, тяжелее и весит от 120 до 130 фунтов (от 54 до 58 кг) на кубический фут.
Правда ли, что звезд больше, чем песка?
Ученые утверждают, что звезд на ночном небе в 10 раз больше, чем песчинок в пустынях и на пляжах мира. Астрономы выяснили, что существует 70 миллиардов миллионов миллионов миллионов — или семь с 22 нулями — звезд, видимых с Земли в телескопы.
На Земле больше песка, чем звезд?
Ученые подсчитали, что Земля содержит 7.5 секстиллионов песчинок. Это 75, за которыми следуют 17 нулей. Это много песка. По оценкам астрономов, на каждую песчинку на Земле приходится примерно 10 000 звезд.
Сколько весит один грамм песка?
Вес различных песчинок варьируется от 0,017 до 0,011 грамма. Песок делится на 5 различных категорий размера зерна.
Сколько весит 5-галлонное ведро песка?
В конечном счете, это зависит от содержания влаги и типа песка.Сколько весит 5-галлонное ведро песка? 5-галлонное ведро песка весит примерно 68 фунтов (31 кг). Сколько весит песчинка? Песок делится на 5 различных категорий размера зерна. Эти категории включают:
Сколько весит песчинка? Песок делится на 5 различных категорий размера зерна. Эти категории включают:
Сколько песчинок в литре песка?
Это будет означать 200 х 200 х 200 зерен в литре. То есть 8 млн. Чашка обычно считается объемом 250 мл. Итак, в этой чашке должно быть не менее 2 миллионов зерен. Исходя из этого расчета, в кубометре песка будет не менее 8…
Сколько зерен в фунте зерна?
Зерно на самом деле является мерой веса, что означает, что вычисление количества зерен в фунте является простым преобразованием веса.1 фунт равен 7000 зерен, и независимо от того, какие зёрнышки приходят, их всё равно будет одинаковое количество на 1 фунт.
Сколько песчинок на пляжах Земли?
Чувак-математик: быстрые и грязные советы, как упростить математику
Scientific American представляет Math Dude от Quick & Dirty Tips. Scientific American и Quick & Dirty Tips принадлежат компаниям Macmillan.
Scientific American и Quick & Dirty Tips принадлежат компаниям Macmillan.
Сегодня мы узнаем, как математика позволяет легко оценивать вещи, которые, казалось бы, практически невозможно рассчитать.В частности, поскольку лето в самом разгаре, мы возьмем математику на пляж и подумаем над извечным вопросом: сколько песчинок на всех пляжах Земли? Как помнят давние поклонники Math Dude, мы впервые узнали об использовании математики для оценок, когда наблюдали за тем, как Secret Agent Math смело подсчитывает, сколько вдохов воздуха в закрытой комнате. Так почему же мы возвращаемся к этой теме? Потому что научиться сочетать свой мозг с математикой для оценки — абсолютно бесценный навык, и этот навык развивается только с практикой.Чем мы и займемся сегодня.
Шаг 1: составьте план Иногда интересно сразу же прыгнуть и сделать что-то, даже не зная, что вы делаете. И хотя такая спонтанность отлично подходит для таких вещей, как лепка из пластилина и спонтанные поездки на выходные, это действительно плохая идея для решения математических задач. Таким образом, первое, что нам нужно сделать сегодня, — это составить план, чтобы выяснить, сколько песчинок на пляжах Земли. Я знаю, что это может показаться почти невыполнимой задачей, но будьте уверены, что преодоление этих, казалось бы, больших шансов — и чувство страха, которое они вселяют в сердца храбрых в других отношениях — это именно то, что сделает наш план.
Таким образом, первое, что нам нужно сделать сегодня, — это составить план, чтобы выяснить, сколько песчинок на пляжах Земли. Я знаю, что это может показаться почти невыполнимой задачей, но будьте уверены, что преодоление этих, казалось бы, больших шансов — и чувство страха, которое они вселяют в сердца храбрых в других отношениях — это именно то, что сделает наш план.
Лучший способ решить такую сложную задачу — разбить ее на более простые части. В нашем случае, если мы можем оценить, сколько песчинок содержится в типичном объеме пляжа (скажем, количество песчинок на кубический метр), а затем оценить, каков объем песка на всех пляжах мира (скажем, в кубических метрах), то все, что нам нужно сделать, чтобы найти общее количество песчинок, — это перемножить эти два числа вместе. Легко, верно? Ну, ладно… возможно, это все еще не совсем просто.Но давайте продолжим смело идти вперед, чтобы посмотреть, сможем ли мы решить каждую из этих подзадач по отдельности, а затем посмотрим, может ли этот подход «разделяй и властвуй» помочь сделать невозможное возможным.
> Продолжить чтение на QuickAndDirtyTips.com
ОБ АВТОРЕ(АХ)
Джейсон Маршалл, доктор философии, ученый-исследователь, автор книг The Math Dude’s Quick and Dirty Guide to Algebra, и ведущий подкаста Math Dude на Quick and Dirty Tips.
Последние статьи математика Джейсона Маршалла
Читать далее
Информационный бюллетень
Будьте умнее. Подпишитесь на нашу новостную е-мэйл рассылку.
Поддержка научной журналистики
Откройте для себя науку, которая изменит мир. Изучите наш цифровой архив с 1845 года, включая статьи более 150 лауреатов Нобелевской премии.
Подпишитесь прямо сейчас!Калькулятор объема
Ниже приведен список калькуляторов объема для нескольких распространенных форм. Пожалуйста, заполните соответствующие поля и нажмите кнопку «Рассчитать».
Калькулятор объема сферы
Калькулятор объема конуса
Калькулятор объема куба
Калькулятор объема цилиндра
Калькулятор объема прямоугольного резервуара
Калькулятор объема капсулы
Калькулятор объема сферической крышки
Укажите любые два значения ниже для расчета.
Калькулятор объема усеченного конуса
Калькулятор объема эллипсоида
Калькулятор объема квадратной пирамиды
Калькулятор объема пробирки
Калькулятор площади поверхности | Калькулятор площади
Объем – это количественная оценка трехмерного пространства, занимаемого веществом.Единицей объема в СИ является кубический метр, или м 3 . По соглашению объем контейнера обычно представляет собой его вместимость и количество жидкости, которое он может вместить, а не объем пространства, которое вытесняет фактический контейнер. Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы можно разбить на более простые совокупные формы, и сумма их объемов используется для определения общего объема. Объемы других, еще более сложных форм, можно рассчитать с помощью интегрального исчисления, если существует формула для границы формы.Помимо этого, формы, которые не могут быть описаны известными уравнениями, могут быть оценены с использованием математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.
Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы можно разбить на более простые совокупные формы, и сумма их объемов используется для определения общего объема. Объемы других, еще более сложных форм, можно рассчитать с помощью интегрального исчисления, если существует формула для границы формы.Помимо этого, формы, которые не могут быть описаны известными уравнениями, могут быть оценены с использованием математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.
Сфера
Сфера — это трехмерный аналог двумерного круга. Это идеально круглый геометрический объект, который математически представляет собой набор точек, равноудаленных от данной точки в его центре, где расстояние между центром и любой точкой на сфере равно радиусу r . Вероятно, наиболее известным сферическим объектом является идеально круглый шар. В математике существует различие между шаром и сферой, где шар представляет собой пространство, ограниченное сферой. Независимо от этого различия, шар и сфера имеют одинаковый радиус, центр и диаметр, и вычисление их объемов одинаково. Как и в случае с окружностью, самый длинный отрезок, соединяющий две точки сферы через ее центр, называется диаметром d . Уравнение для расчета объема сферы приведено ниже:
Вероятно, наиболее известным сферическим объектом является идеально круглый шар. В математике существует различие между шаром и сферой, где шар представляет собой пространство, ограниченное сферой. Независимо от этого различия, шар и сфера имеют одинаковый радиус, центр и диаметр, и вычисление их объемов одинаково. Как и в случае с окружностью, самый длинный отрезок, соединяющий две точки сферы через ее центр, называется диаметром d . Уравнение для расчета объема сферы приведено ниже:
EX: Клэр хочет наполнить идеально сферический шарик с водой радиусом 0.15 футов с уксусом, чтобы использовать его в битве с водяным шаром против ее заклятого врага Хильды в ближайшие выходные. Необходимый объем уксуса можно рассчитать по приведенному ниже уравнению:
объем = 4/3 × π × 0,15 3 = 0,141 фута 3
Конус
Конус представляет собой трехмерную форму, которая плавно сужается от своего обычно круглого основания к общей точке, называемой вершиной (или вершиной). Математически конус образован подобно кругу набором отрезков, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, содержащую круг (или какое-либо другое основание).На этой странице рассматривается только случай конечного прямого кругового конуса. Конусы, состоящие из полулиний, некруглых оснований и т. д., которые простираются до бесконечности, рассматриваться не будут. Уравнение для расчета объема конуса выглядит следующим образом:
Математически конус образован подобно кругу набором отрезков, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, содержащую круг (или какое-либо другое основание).На этой странице рассматривается только случай конечного прямого кругового конуса. Конусы, состоящие из полулиний, некруглых оснований и т. д., которые простираются до бесконечности, рассматриваться не будут. Уравнение для расчета объема конуса выглядит следующим образом:
где r радиус и h высота конуса
EX: Беа полна решимости выйти из магазина мороженого с хорошо потраченными с трудом заработанными 5 долларами. Хотя она предпочитает обычные сахарные рожки, вафельные рожки, бесспорно, крупнее.Она определяет, что на 15 % предпочитает обычные сахарные рожки вафельным рожкам, и ей необходимо определить, превышает ли потенциальный объем вафельного рожка на ≥ 15 % объем сахарного рожка. Объем вафельного рожка с круглым основанием радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать с помощью приведенного ниже уравнения:
объем = 1/3 × π × 1,5 2 × 5 = 11,781 дюйма 3
Беа также вычисляет объем сахарного рожка и обнаруживает, что разница составляет < 15%, и решает купить сахарный рожок. Теперь все, что ей нужно сделать, это использовать свою ангельскую детскую привлекательность, чтобы заставить персонал опустошить контейнеры с мороженым в ее рожок.
Теперь все, что ей нужно сделать, это использовать свою ангельскую детскую привлекательность, чтобы заставить персонал опустошить контейнеры с мороженым в ее рожок.
Куб
Куб является трехмерным аналогом квадрата и представляет собой объект, ограниченный шестью квадратными гранями, три из которых сходятся в каждой из его вершин и все перпендикулярны соответствующим смежным граням. Куб является частным случаем многих классификаций фигур в геометрии, включая квадратный параллелепипед, равносторонний кубоид и правильный ромбоэдр.Ниже приведено уравнение для расчета объема куба:
объем = 3
где a длина ребра куба
ПРИМЕР: Боб, родившийся в Вайоминге (и никогда не покидавший штат), недавно посетил родину своих предков в Небраске. Потрясенный великолепием Небраски и окружающей средой, не похожей ни на что другое, с чем он когда-либо сталкивался, Боб понял, что ему нужно привезти часть Небраски домой с собой. У Боба есть кубический чемодан с длиной ребра 2 фута, и он рассчитывает объем почвы, который он может унести с собой домой, следующим образом:
объем = 2 3 = 8 футов 3
Цилиндр
Цилиндр в его простейшей форме определяется как поверхность, образованная точками на фиксированном расстоянии от заданной прямой оси. Однако в обычном употреблении термин «цилиндр» относится к прямолинейному круговому цилиндру, основаниями которого являются окружности, соединенные через их центры осью, перпендикулярной плоскостям его оснований, с заданной высотой 90 209 h 90 210 и радиусом 90 209 r 90 210. . Уравнение для расчета объема цилиндра показано ниже:
Однако в обычном употреблении термин «цилиндр» относится к прямолинейному круговому цилиндру, основаниями которого являются окружности, соединенные через их центры осью, перпендикулярной плоскостям его оснований, с заданной высотой 90 209 h 90 210 и радиусом 90 209 r 90 210. . Уравнение для расчета объема цилиндра показано ниже:
объем = πr 2 ч
где r радиус и h высота
EX: Кэлум хочет построить замок из песка в гостиной своего дома.Поскольку он является твердым сторонником переработки отходов, он нашел три цилиндрические бочки с незаконной свалки и очистил их от химических отходов, используя средство для мытья посуды и воду. Каждая бочка имеет радиус 3 фута и высоту 4 фута, и Кэлум определяет объем песка, который может вместить каждая, используя приведенное ниже уравнение:
объем = π × 3 2 × 4 = 113,097 футов 3
Он успешно строит замок из песка в своем доме, и в качестве дополнительного бонуса ему удается экономить электроэнергию на ночном освещении, так как его замок из песка светится ярко-зеленым в темноте.
Прямоугольный бак
Прямоугольный резервуар представляет собой обобщенную форму куба, стороны которого могут иметь различную длину. Он ограничен шестью гранями, три из которых сходятся в его вершинах и все перпендикулярны соответствующим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:
объем = длина × ширина × высота
EX: Дарби любит торт. Она ходит в спортзал по 4 часа в день, каждый день, чтобы компенсировать свою любовь к тортам.Она планирует пройти по тропе Калалау на Кауаи, и, хотя Дарби в отличной форме, она беспокоится о своей способности пройти тропу из-за отсутствия торта. Она решает упаковать только самое необходимое и хочет наполнить свой идеально прямоугольный пакет длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно тортом. Точный объем торта, который она может поместить в свою упаковку, рассчитывается ниже:
.объем = 2 × 3 × 4 = 24 фута 3
Капсула
Капсула представляет собой трехмерную геометрическую форму, состоящую из цилиндра и двух полусферических концов, где полусфера представляет собой половину сферы. Отсюда следует, что объем капсулы можно рассчитать, комбинируя уравнения объема для сферы и прямого кругового цилиндра:
Отсюда следует, что объем капсулы можно рассчитать, комбинируя уравнения объема для сферы и прямого кругового цилиндра:
| объем = πr 2 ч + | πr 3 = πr 2 ( | р + ч) |
где r — радиус, а h — высота цилиндрической части
EX: Учитывая капсулу радиусом 1,5 фута и высотой 3 фута, определите объем m&m’s из расплавленного молочного шоколада, который Джо может унести в капсуле времени, которую он хочет закопать для будущих поколений в своем путешествии самопознания через Гималаи:
объем = π × 1.5 2 × 3 + 4/3 ×π ×1,5 3 = 35,343 фута 3
Сферический колпачок
Сферический колпак представляет собой часть сферы, отделенную от остальной части сферы плоскостью. Если плоскость проходит через центр сферы, сферическая шапка называется полусферой. Существуют и другие различия, в том числе сферический сегмент, где сфера сегментирована двумя параллельными плоскостями и двумя разными радиусами, где плоскости проходят через сферу. Уравнение для расчета объема сферического колпака выводится из уравнения для сферического сегмента, где второй радиус равен 0.Относительно сферической крышки, показанной в калькуляторе:
Существуют и другие различия, в том числе сферический сегмент, где сфера сегментирована двумя параллельными плоскостями и двумя разными радиусами, где плоскости проходят через сферу. Уравнение для расчета объема сферического колпака выводится из уравнения для сферического сегмента, где второй радиус равен 0.Относительно сферической крышки, показанной в калькуляторе:
Имея два значения, предоставленный калькулятор вычисляет третье значение и объем. Уравнения для преобразования между высотой и радиусом показаны ниже:
Даны r и R : h = R ± √R 2 — r 2
где r — радиус основания, R — радиус сферы, h — высота сферического колпачка
EX: Джек действительно хочет победить своего друга Джеймса в игре в гольф, чтобы произвести впечатление на Джилл, и вместо того, чтобы тренироваться, он решает саботировать мяч для гольфа Джеймса. Он отрезает идеальный сферический колпачок от мяча для гольфа Джеймса и должен рассчитать объем материала, необходимого для замены сферического колпачка и смещения веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:
Он отрезает идеальный сферический колпачок от мяча для гольфа Джеймса и должен рассчитать объем материала, необходимого для замены сферического колпачка и смещения веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:
объем = 1/3 × π × 0,3 2 (3 × 1,68 — 0,3) = 0,447 дюйма 3
К несчастью для Джека, Джеймс получил новую партию мячей за день до игры, и все усилия Джека оказались напрасными.
Коническая усеченная часть
Коническая усеченная часть — это часть твердого тела, остающаяся после разрезания конуса двумя параллельными плоскостями. Этот калькулятор вычисляет объем для прямого круглого конуса специально. Типичные усеченные конусы, встречающиеся в повседневной жизни, включают абажуры, ведра и некоторые стаканы. Объем правой конической усеченной части рассчитывается по следующему уравнению:
| объем = | πh(r 2 + rR + R 2 ) |
где r и R — радиусы оснований, h — высота усеченного конуса
EX: Беа успешно добыла немного мороженого в сахарном рожке и только что съела его таким образом, что мороженое осталось упакованным внутри рожка, а поверхность мороженого параллельна плоскости отверстия рожка. Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее рожок и откусывает часть нижней части рожка, которая идеально параллельна ранее единственному отверстию. Беа теперь осталась с правым коническим усеченным мороженым, и ей нужно рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченного конуса 4 дюйма и радиусы 1,5 дюйма и 0,2 дюйма:
Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее рожок и откусывает часть нижней части рожка, которая идеально параллельна ранее единственному отверстию. Беа теперь осталась с правым коническим усеченным мороженым, и ей нужно рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченного конуса 4 дюйма и радиусы 1,5 дюйма и 0,2 дюйма:
объем = 1/3 × π × 4 (0,2 2 + 0,2 × 1,5 + 1,5 2 ) = 10.849 в 3
Эллипсоид
Эллипсоид — это трехмерный аналог эллипса и поверхность, которую можно описать как деформацию сферы путем масштабирования направленных элементов. Центром эллипсоида называется точка, в которой пересекаются три попарно перпендикулярные оси симметрии, а отрезки, ограничивающие эти оси симметрии, называются главными осями. Если все три имеют разную длину, эллипсоид обычно называют трехосным.Уравнение для расчета объема эллипсоида выглядит следующим образом:
где a , b и c длины осей
EX: Хабат любит есть только мясо, но его мать настаивает на том, что он ест слишком много, и разрешает ему есть столько мяса, сколько он может поместиться в булочке в форме эллипсоида. Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может поместить в свой бутерброд. Учитывая, что осевая длина его булочки составляет 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат вычисляет объем мяса, который он может поместить в каждую выдолбленную булочку, следующим образом:
Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может поместить в свой бутерброд. Учитывая, что осевая длина его булочки составляет 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат вычисляет объем мяса, который он может поместить в каждую выдолбленную булочку, следующим образом:
объем = 4/3 × π × 1.5 × 2 × 5 = 62,832 дюйма 3
Квадратная пирамида
Пирамида в геометрии — это трехмерное тело, образованное путем соединения многоугольного основания с точкой, называемой его вершиной, где многоугольник — это фигура на плоскости, ограниченная конечным числом прямых отрезков. Существует множество возможных многоугольных оснований для пирамиды, но квадратная пирамида — это пирамида, в которой основание — квадрат. Другое различие, связанное с пирамидами, связано с расположением вершины. Вершина правильной пирамиды находится прямо над центром тяжести ее основания.Независимо от того, где находится вершина пирамиды, если ее высота измеряется как перпендикулярное расстояние от плоскости, содержащей основание, до ее вершины, объем пирамиды можно записать как:
Обобщенный объем пирамиды:
где b площадь основания и h высота
Объем квадратной пирамиды:
, где a — длина ребра основания
EX: Ван очарован древним Египтом и особенно любит все, что связано с пирамидами. Будучи старшим из своих братьев и сестер Ту, Три и Форе, он может легко загнать их в загон и использовать по своему желанию. Воспользовавшись этим, Ван решает воспроизвести древние египетские времена и попросить своих братьев и сестер выступить в роли рабочих, строящих ему пирамиду из грязи с длиной ребра 5 футов и высотой 12 футов, объем которой можно рассчитать с помощью уравнения для квадрата. пирамида:
Будучи старшим из своих братьев и сестер Ту, Три и Форе, он может легко загнать их в загон и использовать по своему желанию. Воспользовавшись этим, Ван решает воспроизвести древние египетские времена и попросить своих братьев и сестер выступить в роли рабочих, строящих ему пирамиду из грязи с длиной ребра 5 футов и высотой 12 футов, объем которой можно рассчитать с помощью уравнения для квадрата. пирамида:
объем = 1/3 × 5 2 × 12 = 100 футов 3
Трубчатая пирамида
Трубка, часто также называемая трубой, представляет собой полый цилиндр, который часто используется для передачи жидкостей или газов.Вычисление объема трубы по существу использует ту же формулу, что и для цилиндра ( объем = pr 2 h ), за исключением того, что в этом случае используется диаметр, а не радиус, и длина используется, а не высота. Таким образом, формула включает измерение диаметров внутреннего и внешнего цилиндров, как показано на рисунке выше, вычисление каждого из их объемов и вычитание объема внутреннего цилиндра из объема внешнего. С учетом использования длины и диаметра, упомянутых выше, формула для расчета объема трубы показана ниже:
С учетом использования длины и диаметра, упомянутых выше, формула для расчета объема трубы показана ниже:
, где d 1 — внешний диаметр, d 2 — внутренний диаметр, а l — длина трубы
EX: Beulah занимается защитой окружающей среды.Ее строительная компания использует только самые экологически чистые материалы. Она также гордится тем, что удовлетворяет потребности клиентов. У одного из ее клиентов есть загородный дом, построенный в лесу, через ручей. Он хочет более легкого доступа к своему дому и просит Беулу построить ему дорогу, обеспечив при этом свободное течение ручья, чтобы не мешать его любимому месту рыбалки. Она решает, что надоедливые бобровые плотины были бы хорошей точкой для прокладки трубы через ручей. Объем запатентованного ударопрочного бетона, необходимый для строительства трубы наружным диаметром 3 фута, внутренним диаметром 2.5 футов и длину 10 футов можно рассчитать следующим образом:
| объем = π × | × l0 = 21,6 фута 3 |
Общие единицы объема
90 076 000473
000473От 1000000 до Число Грэма — Подождите, но Почему
Добро пожаловать в пост номер 2.
На прошлой неделе мы начали с 1 и медленно и неуклонно шли к 1 000 000. Мы использовали точки. Это было мило.
Время веселья закончилось. Сегодня дерьмо становится реальным.
Прежде, чем ситуация полностью выйдет из-под контроля, давайте начнем с того, что поработаем над еще непостижимыми степенями числа 10—
.
Степени числа 10
Когда мы перешли от 1 к 1 000 000, нам не нужны были степени — мы могли просто использовать короткую строку цифр для представления чисел, о которых мы говорили.Если мы хотели умножить число на 10, мы просто прибавляли ноль.
Но по мере того, как вы приближаетесь к миллиону, нулей становится много, и вам нужно другое обозначение. Вот почему мы используем силы. Когда люди говорят об экспоненциальном росте, они имеют в виду сумасшествие, которое может произойти, когда вы начинаете использовать силы. Например:
Если вы умножите 9 845 625 675 438 на 8 372 745 993 275, результат будет меньше, чем 8 29 .
Поскольку сегодня мы становимся все больше и больше, мы будем придерживаться степеней 10, потому что, когда вы начинаете говорить о действительно больших числах, становится важным количество цифр, а не сами цифры, т.е.е. каждое 70-значное число находится где-то между 10 69 и 10 70 , и это все, что вам нужно знать. Так что, по крайней мере, для первой части этого поста степени 10 могут прекрасно служить «контрольными точками» порядка величины.
Так что, по крайней мере, для первой части этого поста степени 10 могут прекрасно служить «контрольными точками» порядка величины.
Каждый раз, когда мы повышаем мощность на единицу, мы умножаем мир, в котором находимся, на десять, существенно меняя ситуацию. Начнем с того, на чем остановились в прошлый раз —
.10 6 (1 миллион – 1 000 000) – Количество точек на том огромном изображении, которое мы закончили на прошлой неделе.На экране моего компьютера это изображение было примерно 18 см x 450 см = 0,81 м 2 по площади.
10 7 (10 миллионов) – Это приводит нас к диапазону, включающему количество шагов, необходимых для обхода Земли (40 миллионов шагов). Если бы каждый из ваших шагов вокруг Земли был представлен точкой, как на сетке в последнем посте, точки заполнили бы квадрат 6 х 6 м.
10 8 (100 миллионов) – Теперь мы находимся на уровне количества книг, когда-либо изданных в истории человечества (130 миллионов), а на вершине этого диапазона находится оценочное количество слов, которое человек произносит за один раз. на всю жизнь (860 миллионов).Также в этом диапазоне находятся шансы на выигрыш в действительно крупных лотереях. В недавней лотерее Mega Millions шансы на выигрыш составляли 1 к 175 711 536. Чтобы представить эти шансы в перспективе, это примерно количество секунд за шесть лет. Так что это все равно, что знать, что ежик чихнет один и только один раз в следующие шесть лет, и ставить свои с трудом заработанные деньги на одну конкретную секунду — скажем, на 36-й секунде 2:52 утра 19 марта 2017 года — и выигрывать только в том случае, если один чих происходит ровно в эту секунду. Не покупайте билет Mega Millions.
на всю жизнь (860 миллионов).Также в этом диапазоне находятся шансы на выигрыш в действительно крупных лотереях. В недавней лотерее Mega Millions шансы на выигрыш составляли 1 к 175 711 536. Чтобы представить эти шансы в перспективе, это примерно количество секунд за шесть лет. Так что это все равно, что знать, что ежик чихнет один и только один раз в следующие шесть лет, и ставить свои с трудом заработанные деньги на одну конкретную секунду — скажем, на 36-й секунде 2:52 утра 19 марта 2017 года — и выигрывать только в том случае, если один чих происходит ровно в эту секунду. Не покупайте билет Mega Millions.
10 9 (1 миллиард 1 – 1 000 000 000) – Здесь мы имеем количество секунд в столетии (около 3 миллиардов), количество живущих людей (7,125 миллиарда), и чтобы уместить миллиард точек, наше точечное изображение охватило бы две баскетбольные площадки.
10 10 (10 миллиардов) – Теперь мы подошли к количеству лет, прошедших после Большого Взрыва (13,7 миллиардов), и количеству секунд, прошедших с тех пор, как жил Иисус Христос (60 миллиардов).
10 11 (100 миллиардов) – Это примерно количество звезд в Млечном Пути и количество галактик в наблюдаемой Вселенной (100-400 миллиардов) Боже, в настоящее время это далеко не закончено.
10 12 (1 триллион – 1 000 000 000 000) – Миллион миллионов. Количество фунтов, которое покажут весы, если вы поместите на них всю человеческую расу (~ 1 триллион), количество секунд, в течение которых люди существуют (~ 100 000 лет = ~ 3 триллиона секунд), и больше, чем обе эти суммы вместе взятые. , количество миль в одном световом году (6 трлн). Триллион настолько велик, что вам понадобится всего 4 триллиона миллиметров ленты, чтобы завязать бантик вокруг солнца.
10 13 (10 триллионов) – Это примерно столько, сколько мы можем получить для чисел, которые мы слышим в реальном мире, и это почти всегда связано с нациями и долларами — номинальный ВВП США в 2013 году был чуть ниже 17 триллионов долларов, а его долг в настоящее время составляет чуть менее 18 триллионов долларов. Оба они ничтожны по количеству клеток в человеческом теле (37 триллионов).
Оба они ничтожны по количеству клеток в человеческом теле (37 триллионов).
10 14 (100 триллионов) – 100 триллионов – это примерно количество букв в каждой изданной книге в истории человечества, а также количество бактерий в вашем теле.2 Также в этом диапазоне находится общее богатство мире (241 трлн долларов, которые мы подробно обсуждали в предыдущем посте).
10 15 (1 квадриллион) – Ладно, до свидания нормальные слова. Люди часто произносят слова «миллион», «миллиард» и «триллион».Никто не говорит квадриллион. Говорить слово «квадриллион» на самом деле не круто3. Большинство людей вместо этого выбирают «миллион миллиардов». В любом случае, на Земле около квадриллиона муравьев. Сравнивая это с фактом о бактериях, у вас внутри ползает 1/10 часть всех муравьев мира.
10 16 (10 квадриллионов) – Именно в этом диапазоне мы получаем количество игральных карт, которое нужно случайно сбить со стола, чтобы покрыть всю Землю (89 квадриллионов). Люди будут злиться на вас.
Люди будут злиться на вас.
10 17 (100 квадриллионов) – Количество секунд с момента Большого Взрыва. Также количество упоминаний Ким Кардашьян, которые появились в моем звуковом ландшафте за последнюю неделю. Пожалуйста остановись.
10 18 (1 квинтиллион) – Также известное как миллиард миллиардов, слово квинтиллион еще менее круто, чем квадриллион. Никто из тех, кто обладает социальными навыками, никогда не произносит слово «квинтиллион». Во всяком случае, это количество кубометров воды во всех океанах Земли и количество атомов в крупице соли (1.2 квинтиллиона). Количество песчинок на каждом пляже Земли составляет около 7,5 квинтиллионов — столько же атомов содержится в шести песчинках соли .
10 19 (10 квинтиллионов) – Количество миллиметров отсюда до ближайшей следующей звезды (38 квинтиллионов миллиметров).
10 20 (100 квинтиллионов) – Количество метровых шагов, которое вам потребуется, чтобы пройти весь Млечный Путь. Так много подкастов. Вы слышали о томе Планка? Это наименьший объем, о котором говорят ученые, настолько маленький, что вы могли бы поместить 100 квинтиллионов из них в протон .Подробнее о планковских томах позже. О, а наше точечное изображение? К тому времени, когда мы доберемся до 600 квинтиллионов точек, изображение покроет поверхность Земли.
Так много подкастов. Вы слышали о томе Планка? Это наименьший объем, о котором говорят ученые, настолько маленький, что вы могли бы поместить 100 квинтиллионов из них в протон .Подробнее о планковских томах позже. О, а наше точечное изображение? К тому времени, когда мы доберемся до 600 квинтиллионов точек, изображение покроет поверхность Земли.
10 21 (1 секстиллион) – Теперь мы даже за пределами словарного запаса чудаков. Я не думаю, что когда-либо слышал, чтобы кто-то произносил вслух «секстиллион», и я надеюсь, что так и останется.
10 23 (100 секстиллионов) – Грубая оценка количества звезд в наблюдаемой Вселенной.Вам также приходилось иметь дело с этим числом в старшей школе — 602 секстиллиона, или 6,02 х 10 23 — это моль, или число Авогадро, и количество атомов водорода в грамме водорода.
10 24 (1 септиллион) – Триллион триллионов. Земля весит около шести септиллионов килограммов.
Земля весит около шести септиллионов килограммов.
10 25 (10 септиллион) – Количество капель воды во всех океанах мира.
10 27 (1 октиллион) – Если бы Земля была полой, то для ее заполнения потребовался бы 1 октиллион горошин.И я думаю, что мы достаточно услышали от octillion.
Хорошо, а теперь давайте совершим огромный скачок вперед на совершенно другую территорию — туда, где объем Земли слишком мал, а Большой взрыв слишком недавний, чтобы использовать его в примерах. На этой новой арене чисел только наблюдаемая Вселенная — сфера диаметром около 92 миллиардов световых лет — может справиться с величиной, с которой мы имеем дело.4
10 80 – Чтобы получить 10 80 , вы берете триллион и умножаете его на триллион, на триллион, на триллион, на триллион, на триллион, на сто миллионов.Плакаты с точками для этого номера не продаются. Так почему же я остановился на этом номере? Потому что это общепринятая оценка количества атомов во Вселенной.
10 86 – А что, если бы вы захотели засыпать горохом всю обозримую вселенную сферу? Для этого вам понадобится 10 86 горошин.
10 90 – Вот сколько песчинок среднего размера (0,5 мм в диаметре) потребуется, чтобы заполнить Вселенную.
А Гугол – 10 100
Название гугол появилось, когда однажды в 1938 году американский математик Эдвард Каснер проявил милость и попросил своего 9-летнего племянника Милтона придумать имя для 10 100 -1 со 100 нулями.Милтон, будучи глупым 9-летним ребенком, предложил «гугол». Каснер, очевидно, решил, что это разумный ответ, согласился с ним, и на этом все.
Итак, насколько велик гугол?
— это количество песчинок, которые могут поместиться во Вселенной, умноженное на 10 миллиардов. Итак, представьте себе Вселенную, битком набитую мелкими песчинками — на десятки миллиардов световых лет над Землей, под ней, перед ней, позади нее — просто песок. Бесконечный песок. Вы можете пролететь над ним на самолете триллионы лет в любом направлении на полной скорости, и вы никогда не доберетесь до края песка.Много-много-много песка.
Бесконечный песок. Вы можете пролететь над ним на самолете триллионы лет в любом направлении на полной скорости, и вы никогда не доберетесь до края песка.Много-много-много песка.
А теперь представьте, что вы останавливаете самолет в какой-то момент, протягиваете руку к окну и берете одну песчинку, чтобы рассмотреть ее под мощным микроскопом, и вы видите, что на самом деле это не одна песчинка, а 10 миллиардов микроскопических песчинок, обернутых друг в друга. в мембране, все вместе размером с нормальную песчинку. Если бы это было так для каждой отдельной песчинки в этой гипотезе — если бы каждая песчинка была на самом деле связкой из 10 миллиардов мельчайших песчинок — общее количество этих микроскопических песчинок было бы гуголом.
У нас не хватает места как для малого, так и для большого числа вещей, чтобы вписать эти числа в физический мир, но для вас есть еще три:
10 113 – Количество атомов водорода, необходимое для заполнения ими Вселенной.
10 122 – Количество протонов, которое может поместиться во Вселенной.
10 185 – Назад к планковскому объему (самому маленькому объему, который я когда-либо слышал в научных обсуждениях).Сколько из этих самых маленьких вещей вы могли бы поместить в самую большую вещь, наблюдаемую вселенную? 10 185 . Не имея возможности ни уменьшаться, ни увеличиваться с обеих сторон, мы достигли наибольшего числа, когда физический мир можно использовать для его визуализации.
А Гуголплекс – 10 гугол
После популяризации недавно названного гугола , Краснер еле держался в штанах с этой очаровательной новой фишкой и попросил своего племянника отчеканить еще один термин .Едва он успел закончить вопрос, как Милтон открыл рот, лишенный нюансов, и объявил число гуголплекс , которое он в типичной милтоновской форме описал как «единицу, за которой следует писать нули, пока вы не устанете». проявил некоторую нехарактерную для него сдержанность, проигнорировав Милтона и дав цифре точное определение: 10 гугол или 1 с нулевым гуголом, написанным после него. Гуголплекс с полным выписанным показателем степени выглядит так:
проявил некоторую нехарактерную для него сдержанность, проигнорировав Милтона и дав цифре точное определение: 10 гугол или 1 с нулевым гуголом, написанным после него. Гуголплекс с полным выписанным показателем степени выглядит так:
10 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 до
Итак, гугол — это 1 со 100 нулями после него, что в 10 миллиардов раз больше, чем песчинки, которые заполнили бы Вселенную.Вы можете себе представить, какое число получится, если вы поставите гугола и нуля после единицы?
Невозможно уложить это число в голове — лучшее, что мы можем сделать, — это попытаться понять, сколько времени потребуется, чтобы написать число. То, что я написал выше, — это всего лишь экспонента : на самом деле записывает гуголплекс из , который включает запись нулей гугола. Во-первых, давайте вычислим , где мы запишем эти нули.
То, что я написал выше, — это всего лишь экспонента : на самом деле записывает гуголплекс из , который включает запись нулей гугола. Во-первых, давайте вычислим , где мы запишем эти нули.
Как мы уже говорили, заполнение вселенной песком дает вам только одну миллиардную часть пути к гуголу, поэтому нам нужно заполнить вселенную до краев песком, взять очень маленькую ручку и напишите 10 миллиардов нулей на каждой песчинке .Если бы вы сделали это, а затем посмотрели на законченное зерно под микроскопом, вы бы увидели, что оно покрыто 10 миллиардами микроскопических нулей. Если бы вы проделали это с каждой песчинкой, заполняющей вселенную, вы бы успешно записали число гуголплекс.
И сколько времени это займет?
Ну, я только что проверил, насколько быстро человек может разумно писать нули, и я написал 36 нулей за 10 секунд. за один день, если бы я писал нули с такой скоростью, я бы закончил с половиной песчинки за свою жизнь. Вам нужно посвятить две полные человеческие жизни, чтобы закончить одну песчинку. За всю историю вида на Земле когда-либо жило около 107 миллиардов человек. Если бы каждый человек посвящал каждый момент своей жизни тому, чтобы писать нули на песчинках, мы как биологический вид к настоящему времени заполнили бы куб со стороной 1,7 м (примерно ростом человека) завершенными песчинками. Это это .
Вам нужно посвятить две полные человеческие жизни, чтобы закончить одну песчинку. За всю историю вида на Земле когда-либо жило около 107 миллиардов человек. Если бы каждый человек посвящал каждый момент своей жизни тому, чтобы писать нули на песчинках, мы как биологический вид к настоящему времени заполнили бы куб со стороной 1,7 м (примерно ростом человека) завершенными песчинками. Это это .
Теперь, чтобы получить представление о том, насколько велико реальное число — как объясняют нумерофилы, общее количество возможных квантовых состояний, которые могут возникнуть в пространстве, занимаемом человеком (т.е. каждое возможное расположение атомов, которое может произойти в этом пространстве) на далеко на меньше, чем гуголплекс. Это означает, что если бы существовала вселенная объемом гуголплекс кубических метров (чрезвычайно большое пространство), случайная вероятность предполагает, что в этой вселенной было бы точных копии вас . Почему? Потому что каждое возможное расположение материи в пространстве размером с человека, скорее всего, будет происходить много-много раз в таком огромном пространстве, а это означает, что все, что может существовать, будет существовать, включая вас. Включая тебя с кошачьими усами, но в остальном нормального. Включая тебя, но версию ростом в один фут. Включая вас именно такими, какие вы есть, за исключением того, что вместо мизинца на левой руке у вас там пенис Наполеона в качестве пятого пальца. То, что я говорю, не научная фантастика — это реальность такого большого космоса.
Включая тебя с кошачьими усами, но в остальном нормального. Включая тебя, но версию ростом в один фут. Включая вас именно такими, какие вы есть, за исключением того, что вместо мизинца на левой руке у вас там пенис Наполеона в качестве пятого пальца. То, что я говорю, не научная фантастика — это реальность такого большого космоса.
Номер Грэма
Знаешь, как иногда ты идешь по жизни и теряешься, но даже не подозреваешь об этом, а потом однажды появляется нужный человек, и ты понимаешь, что искал все это время?
Вот как я отношусь к числу Грэма.
Огромные числа всегда и мучили меня, и вызывали у меня кошмары, и, пока я не узнал о числе Грэма, я думал, что самые большие числа, которые может когда-либо вообразить человек, это такие вещи, как «гуголплекс в гуголплексной степени», которые поразили бы меня, когда я Я думал об этом. Но когда я узнал о числе Грэма, я понял, что я не только не поцарапал поверхности действительно огромного числа, я был неспособен сделать это — у меня не было инструментов. И теперь, когда я получил эти инструменты (и вы тоже сегодня), гуголплекс в гуголплексной мощности звучит как ребенок, говорящий «100 плюс 100!» когда его попросили назвать самое большое число, которое он мог придумать.
И теперь, когда я получил эти инструменты (и вы тоже сегодня), гуголплекс в гуголплексной мощности звучит как ребенок, говорящий «100 плюс 100!» когда его попросили назвать самое большое число, которое он мог придумать.
Прежде чем мы углубимся в тему, почему люди говорят о числе Грэма?
Я не буду объяснять это на самом деле, потому что объяснение действительно скучное и запутанное — вот официальная задача, над которой работал Рональд Грэм (живой американский математик), когда он ее придумал:
Соедините каждую пару геометрических вершин n-мерного гиперкуба, чтобы получить полный граф на 2 n вершин. Раскрасьте каждое ребро этого графа красным или синим цветом.При каком наименьшем значении n каждая такая раскраска содержит хотя бы один одноцветный полный подграф на четырех компланарных вершинах?
Я же говорил, что это скучно и запутанно. Как бы то ни было, единого ответа на эту проблему не существует, но доказательство Грэма включает нижнюю и верхнюю границы, а число Грэма было одной из версий верхней границы для n , которую придумал Грэм.
Он придумал это число в 1977 году, и оно получило признание, когда его коллега написал о нем в журнале Scientific American и назвал его «границей настолько огромной, что она является рекордом самого большого числа, когда-либо использовавшегося в серьезном математическом доказательстве».Число попало в Книгу рекордов Гиннесса в 1980 году по той же причине. Вот почему число Грэма так важно — это не просто произвольно огромное число, оно действительно имеет значение в мире математики.
Так или иначе, я сказал выше, что я был ограничен в количестве, которое я мог даже вообразить, потому что у меня не было инструментов — так какие инструменты нам нужны для этого?
На самом деле это один ключевой инструмент: последовательность гиперопераций.
Последовательность гиперопераций — это последовательность математических операций (например, сложение, умножение и т. д.), где каждая операция в последовательности представляет собой итерацию по сравнению с предыдущей операцией. Вы поймете через секунду. Начнем с первой и самой простой операции: подсчета.
Вы поймете через секунду. Начнем с первой и самой простой операции: подсчета.
Рабочий уровень 0 – подсчет
Если у меня 3 и я хочу подняться оттуда, я иду 3, 4, 5, 6, 7 и так далее, пока не доберусь до того места, где хочу быть. Не мощная операция.
Рабочий уровень 1 – Дополнение
Сложение — это итерация вверх от подсчета, которую мы можем назвать «повторяющимся подсчетом», поэтому вместо 3, 4, 5, 6, 7 я могу просто сказать 3 + 4 и сразу перейти к 7. Сложение — это «повторяющийся подсчет». ” означает, что сложение похоже на сокращение подсчета — способ объединить все шаги подсчета в один, более краткий шаг.
Операционный уровень 2 – Умножение
На один уровень выше умножение является повторяющимся сложением — сокращенный способ сложения.Вместо того, чтобы говорить 3 + 3 + 3 + 3, умножение позволяет нам объединить все эти шаги сложения в один шаг более высокой операции и, скажем, 3 x 4. Умножение — более мощная операция, чем сложение, и с его помощью вы можете создавать гораздо большие числа. . Если я сложу два восьмизначных числа вместе, я получу либо восьмизначное, либо девятизначное число. Но если я умножу на два восьмизначных числа, я получу 15- или 16-значное число — намного больше.
Умножение — более мощная операция, чем сложение, и с его помощью вы можете создавать гораздо большие числа. . Если я сложу два восьмизначных числа вместе, я получу либо восьмизначное, либо девятизначное число. Но если я умножу на два восьмизначных числа, я получу 15- или 16-значное число — намного больше.
Рабочий уровень 3 – Возведение в степень (↑)
При переходе на следующий уровень возведение в степень представляет собой многократное умножение.Вместо того, чтобы говорить 3 x 3 x 3 x 3, возведение в степень позволяет мне связать эту строку в более сжатую 3 4 .
Дело в том, что на этом останавливается большинство людей. В реальном мире возведение в степень — это высшая операция, которую мы склонны когда-либо использовать в последовательности гиперопераций. И когда я представлял себе свое огромное число гуголплекс гуголплекс , я делал все возможное, используя высший известный мне уровень — возведение в степень. На уровне 3 путь к максимальному увеличению состоит в том, чтобы сделать массивным базовое число и число экспоненты массивным.Как только я это сделал, я достиг максимума.
На уровне 3 путь к максимальному увеличению состоит в том, чтобы сделать массивным базовое число и число экспоненты массивным.Как только я это сделал, я достиг максимума.
Ключом к прорыву потолка к действительно большим числам является понимание того, что вы можете подняться на большее количество уровней операций — вы можете бесконечно повторять итерации. Это способ, которым числа становятся по-настоящему огромными.
А для этого нам понадобится другой вид записи. До сих пор мы работали с разными символами на каждом уровне (+, x и надстрочный индекс), но мы не хотим запоминать кучу разных символов, если собираемся работать с кучей символов. разный уровень операций.Поэтому мы будем использовать обозначение Кнута со стрелкой вверх, которое является одним из символов, который можно использовать на любом уровне.
Обозначение Кнута со стрелкой вверх начинается на операционном уровне 3, заменяя возведение в степень одной стрелкой вверх: ↑. Таким образом, используя обозначение со стрелкой вверх, вместо того, чтобы говорить 3 4 , мы говорим 3 ↑ 4, но они означают одно и то же.
Таким образом, используя обозначение со стрелкой вверх, вместо того, чтобы говорить 3 4 , мы говорим 3 ↑ 4, но они означают одно и то же.
3 ↑ 4 = 81
2 ↑ 3 = 8
5 ↑ 5 = 3,125
1 ↑ 38 = 1
Понял? Хорошо.
Теперь давайте поднимемся на уровень выше и начнем видеть безумную мощь последовательности гиперопераций:
Рабочий уровень 4 – Тетрация (↑↑)
Тетрация — это многократное возведение в степень.Прежде чем мы сможем понять, как связать строку возведения в степень так же, как возведение в степень связывает строку умножения, нам нужно понять, что такое «строка возведения в степень».
До сих пор все, что мы сделали с возведением в степень, — это одно вычисление — базовое число и степень, в которую оно возведено. Но что, если мы объединим два этих вычисления, например:
?2 2 2
Получаем силовую башню . Энергетические башни невероятно мощные, потому что они начинаются сверху и спускаются вниз. Итак, 2 2 2 = 2 (2 2 ) = 2 4 = 16. Пока ничего особенного, но посмотрите:
Итак, 2 2 2 = 2 (2 2 ) = 2 4 = 16. Пока ничего особенного, но посмотрите:
3 3 3 3
Использование скобок, чтобы подчеркнуть сверху вниз Заказать: 3 3 3 3 = 3 3 = 3 3 (3 3 ) = 3 3 27 = 3 (3 27 ) = 3 7 625 597 484 987 = 3,6 триллиона — цифра число
Помните, что гугол и его микроскопический мини-песок, заполняющий вселенную, — это всего лишь 100-значное число.Итак, все, что требуется, — это силовая башня из 3-х, сложенных по 4 в высоту, до карлика гугола, а также 10 185 , количество объемов Планка, чтобы максимально заполнить вселенную и наш физический мир. Он не такой большой, как гуголплекс, но мы можем легко позаботиться об этом, просто добавив еще одну 3 в стек:
.
3 3 3 3 3 3 3 = 3 (3 3 (3 3 3 3 ) = 3 (3,6 триллионной цифр) = Путь больше, чем Googolplex, это 10 (100-значное число) .Что же касается самого гуголплекса, то силовые вышки позволяют сразу его унизить, написав так:
10 10 100 или чаще 10 10 10 2 . Итак, вы можете себе представить, какое число вы получите, когда начнете делать высоких силовых башен. Тетрация интенсивная.
Теперь эти башни относятся к экспоненциальным строкам уровня 3, точно так же, как 3 x 3 x 3 x 3 является строкой умножения уровня 2. Мы используем уровень 3, чтобы связать эту строку уровня 2 в 3 4 или 3 ↑ 4.Итак, как мы можем использовать уровень 4 для связывания экспоненциальной строки? Двойные стрелки.
3 3 3 3 — это то же самое, что сказать 3 ↑ (3 ↑ (3 ↑ 3)). Мы объединяем эти 4 тройки с одной стрелкой в 3 ↑↑ 4.
Мы объединяем эти 4 тройки с одной стрелкой в 3 ↑↑ 4.
Аналогично, 3 ↑↑ 5 = 3 ↑ (3 ↑ (3 ↑ (3 ↑ 3))) = 3 3 3 3 3
4 ↑↑ 7 = 4 ↑ (4 ↑ (4 ↑ (4 ↑ (4 ↑ (4 ↑ 4)))))) = силовая башня высотой 4 с 7.
Вот общее правило:
Мы собираемся перейти на следующий уровень, и это должно стать более сложным, поэтому, прежде чем мы двинемся дальше, убедитесь, что вы действительно понимаете Уровень 4 и что означает ↑↑ — просто помните, что ↑↑ b — это силовая башня a’s, b высокая.
Операционный уровень 5 — Pentation (↑↑↑)
Pentation, или повторная тетрация, связывает цепочки двойных стрелок вместе в одну операцию.
Паттерн, который мы видели, состоит в том, что каждый новый уровень связывает вместе строку предыдущего уровня, используя терм b в качестве длины строки. Например:
В каждом случае a — это базовый номер, а b — это длина связываемой строки.
Так что же объединяет Pentation? Как у вас может быть цепочка из силовых башен?
Ответ — то, что я называю «безумным кормлением силовой башни». Вот как это работает:
У вас есть ряд силовых башен, стоящих рядом друг с другом в определенном порядке, и все они используют один и тот же базовый номер. Единственное, что между ними отличается, это высота каждой башни. Высота первой башни равна числу основания. Вы обрабатываете эту башню до ее полного развернутого результата, и этот результат становится высотой следующей башни . Затем вы обрабатываете эту башню, и результатом становится высота следующей башни. И так далее. Результат каждой башни «подпитывается» следующей башней и становится ее высотой — отсюда и безумие подпитки. Вот почему это происходит:
3 ↑↑↑ 4 означает строку из (3 ↑↑ 3) операций длиной 4. Итак:
3 ↑↑↑ 4 = 3 ↑↑ (3 ↑↑ (3 ↑↑ 3))
Помните, когда вы видите ↑↑, это означает одиночную силовую башню высотой b , поэтому:
3 ↑↑↑ 4 = 3 ↑↑ (3 ↑↑ (3 ↑↑ 3)) = 3 ↑↑ (3 ↑↑ 3 3 3 )
Теперь вы, возможно, помните, что 3 3 3 = 3 27 = 7 625 597 484 987. Итак:
Итак:
3 ↑↑↑ 4 = 3 ↑↑ (3 ↑↑ (3 ↑↑ 3)) = 3 ↑↑ (3 ↑↑ 3 3 3 ) = 3 ↑↑ (3 ↑↑ 7,625
Таким образом, первая башня высотой 3 превратилась в 7 триллионов. Теперь следующие скобки, с которыми мы имеем дело, это (3 ↑↑ 7 625 597 484 987), где результат первой башни равен высоте этой второй башни. И какой высоты будет эта башня из 7 триллионов троек?
Что ж, если каждая тройка имеет высоту два сантиметра, а это примерно то же самое, что написанные мною тройки, то башня будет возвышаться примерно на 150 миллионов километров, что коснется солнца.Даже если бы мы использовали крошечные, типа 2 мм 3, наша башня достигла бы Луны и обратно на Землю и обратно на Луну сорок раз, прежде чем закончить. Если бы вместо этого мы написали эти крошечные тройки на земле, башня обернулась бы вокруг земли 400 раз. Назовем эту башню «башней солнца», потому что она простирается до самого солнца. Итак, что у нас есть:
3 ↑↑↑ 4 = 3 ↑↑ (3 ↑↑ (3 ↑↑ 3)) = 3 ↑↑ (3 ↑↑ 3 3 3 ) = 3 ↑↑ (3 ↑↑ 7,625 ↑ (солнечная башня)
Эта последняя операция 3 ↑↑ (солнечная башня) представляет собой силовую башню из 3, высота которой равна числу, которое вы получите, если умножите всю солнечную башню (и эта последняя башня, которую мы строим, даже близко не подходит для наблюдаемая Вселенная). И мы не получим окончательного значения 3 ↑↑↑ 4, пока не умножим на этой последней башни .
И мы не получим окончательного значения 3 ↑↑↑ 4, пока не умножим на этой последней башни .
Таким образом, использование ↑↑↑, или пентаций, вызывает безумие, питающее силовую башню, где по мере продвижения высота каждой башни начинает становиться непонятной, не говоря уже о фактическом конечном значении. Написано вообще:
Поднимемся еще на один уровень —
Уровень операции 6 — Шестигранник (↑↑↑ ↑ )
Итак, на Уровне 4 мы имеем дело с последовательностью экспонентов Уровня 3 — силовой башней.На уровне 5 мы имеем дело с цепочкой силовых башен 4-го уровня — силовой башней, подпитывающей безумие. На уровне 6, также известном как гексация или повторная пентация, мы имеем дело с чередой безумных подпиток силовых башен — то, что мы назовем «фестивалем безумия подпитки силовых башен». Вот основная идея:
Происходит лихорадочное кормление силовой башни. Окончательное число, которое выдает безумие, становится — количество башен в следующем безумии кормления. Затем это безумие происходит и производит еще более смешное число, которое затем становится количеством башен для следующего безумия.И так далее.
Затем это безумие происходит и производит еще более смешное число, которое затем становится количеством башен для следующего безумия.И так далее.
3 ↑↑↑↑ 4 — психо-фестиваль безумия кормления силовой башни, во время которого проводится 3 полных ↑↑↑ безумия кормления, каждое из которых определяет количество башен в следующем. Итак:
3 ↑↑↑↑ 4 = 3 ↑↑↑ (3 ↑↑↑ (3 ↑↑↑ 3))
Теперь помните, что 3 ↑↑↑ 3 превращается в солнечную башню. Итак:
3 ↑↑↑↑ 4 = 3 ↑↑↑ (3 ↑↑↑ (3 ↑↑↑ 3)) = 3 ↑↑↑ (3 ↑↑↑ (солнечная башня))
Поскольку ↑↑↑ означает безумие кормления силовой башни, то, что мы имеем здесь с 3 ↑↑↑ (солнечная башня), является безумием кормления с умноженным числом солнечных башен башен .Когда , кормят , наконец, заканчиваются, результатом становится количество башен в финальном безумии кормления. Психо-фестиваль заканчивается, когда это последнее безумное кормление дает свой последний номер. Вот шестнадцатеричное объяснение в целом:
Вот как работает последовательность гиперопераций. Вы можете продолжать увеличивать количество стрелок, и каждая стрелка, которую вы добавляете , резко взрывает масштаб, с которым вы имеете дело. На данный момент мы прошли первые семь операций в последовательности, включая первые четыре уровня стрелок:
Вы можете продолжать увеличивать количество стрелок, и каждая стрелка, которую вы добавляете , резко взрывает масштаб, с которым вы имеете дело. На данный момент мы прошли первые семь операций в последовательности, включая первые четыре уровня стрелок:
↑ = мощность
↑↑ = силовая башня
↑↑↑ = силовая башня питающееся безумие
↑↑↑↑ = силовая башня кормящее безумие психофестиваль
Итак, теперь, когда у нас есть набор инструментов, давайте пройдемся по номеру Грэма:
Число Грэма будет равно термину g 64 .Мы доберемся туда. Во-первых, нам нужно начать с числа г 1 , а затем мы будем двигаться вверх. Так что же такое g 1 ?
г 1 = 3 ↑↑↑↑ 3
Гексация. Ты понял. Что-то вроде. Итак, давайте пройдемся по нему.
Поскольку стрел четыре, похоже, что у нас в руках силовая башня, питающая фестиваль психопатов безумия. Вот как это выглядит визуально:
Вот как это выглядит визуально:
Итак, g 1 = 3 ↑↑↑↑ 3 = 3 ↑↑↑ (3 ↑↑↑ 3), и у нас есть два повода для беспокойства.Давайте сначала разберемся с первым (красным):
.г 1 = 3 ↑↑↑↑ 3 = 3 ↑↑↑ (3 ↑↑↑ 3) = 3 ↑↑↑ (3 ↑↑ (3 ↑↑ 3))
Итак, это первое безумие кормления состоит из двух ↑↑ силовых башен. Первая башня (синяя) — простая маленькая, потому что значение b составляет всего 3:
.г 1 = 3 ↑↑↑↑ 3 = 3 ↑↑↑ (3 ↑↑↑ 3) = 3 ↑↑↑ (3 ↑↑ (3 ↑↑ 3)) = 3 ↑↑↑ (3 ↑↑ 3) 3 3 )
И мы узнали, что 3 3 3 = 7 625 597 484 987, значит:
г 1 = 3 ↑↑↑↑ 3 = 3 ↑↑↑ (3 ↑↑↑ 3) = 3 ↑↑↑ (3 ↑↑ (3 ↑↑ 3)) = 3 ↑↑↑ (3 ↑↑ 3) 3 3 ) = 3 ↑↑↑ (3 ↑↑ 7 625 597 484 987)
И мы знаем, что (3 ↑↑ 7 625 597 484 987) наша солнечная башня высотой 150 км:
г 1 = 3 ↑↑↑↑ 3 = 3 ↑↑↑ (3 ↑↑↑ 3) = 3 ↑↑↑ (3 ↑↑ (3 ↑↑ 3)) = 3 ↑↑↑ (3 ↑↑ 3) 3 3 ) = 3 ↑↑↑ (3 ↑↑ 7 625 597 484 987) = 3 ↑↑↑ (солнечная башня)
Чтобы очистить его:
г 1 = 3 ↑↑↑↑ 3 = 3 ↑↑↑ (3 ↑↑↑ 3) = 3 ↑↑↑ (солнечная башня)
Итак, после первого из двух безумных кормлений у нас осталась эпически высокая солнечная башня из 3, которую нужно умножить. Помните, как ранее мы показывали, как быстро растет силовая вышка:
Помните, как ранее мы показывали, как быстро растет силовая вышка:
3 = 3
3 3 = 27 3 = 27 3 = 7 60047 = 7 625 597 484 987 3 3 3 3 = 3,6 триллионного цифра, пусть больше, чем гуоголь, который будет обернуть Земля пару сотен раз, если вы напишете это
3 3 3 3 3 = число с показателем степени из 3,6 триллиона цифр , намного больше, чем гуголплекс, и число, которое вы могли бы t приблизиться к , записывая в обозримой Вселенной, не говоря уже о том, чтобы умножить
Довольно безумный рост, правда?
И это только верхние несколько сантиметров солнечной башни.
Как только мы опускаемся на метр вниз, число действительно становится намного, намного, намного больше, чем мы когда-либо могли себе представить. А это на метр ниже .
Башня опускается на 150 миллионов километров.
Назовем окончательный результат этой умноженной солнечной башни БЕЗУМИЕ заглавными буквами. Мы не можем понять даже умножения нескольких сантиметров, поэтому 150 миллионов километров будут называться БЕЗУМИЕ, и мы просто будем жить с этим.
Итак, туда, где мы были:
г 1 = 3 ↑↑↑↑ 3 = 3 ↑↑↑ (3 ↑↑↑ 3) = 3 ↑↑↑ (солнечная башня)
И теперь мы можем заменить солнечную башню на окончательный номер, который она производит:
г 1 = 3 ↑↑↑↑ 3 = 3 ↑↑↑ (3 ↑↑↑ 3) = 3 ↑↑↑ (башня солнца) = 3 ↑↑↑ БЕЗУМИЕ
Итак, мы готовы ко второму из двух безумных кормлений. А вот что касается этого второго безумия кормления —
.Итак, вы знаете, как я расстроился из-за всего этого БЕЗУМИЯ?
Это результат лихорадочного кормления всего двумя башнями .Первый маленький размножился и подпитывался вторым, и результатом было БЕЗУМИЕ.
А теперь второе безумное кормление…
Есть БЕЗУМНОЕ число башен .
Мы продолжим через минуту, и я перестану делать эти драматичные абзацы из одного предложения, обещаю, но просто впитайте это на секунду. INSANITY были настолько велики, что о них невозможно было говорить. Планковские объемы во Вселенной — это шутка. Гуголплекс смехотворный. Он слишком велик, чтобы быть частью моей жизни.И это количество башен во втором безумии кормления.
Итак, у нас есть БЕЗУМНОЕ количество башен, каждая из которых умножается на все высоту следующей, пока каким-то образом, где-то, в какой-то момент в будущей вселенной, мы не умножим нашу последнюю башню из это второе безумие кормления… и этот номер — давайте назовем его НЕТ, Я ДАЖЕ НЕ МОГУ — это окончательный результат психофестиваля кормления безумия 3 ↑↑↑↑ 3 силовой башни.
Это число — НЕТ, Я ДАЖЕ НЕ МОГУ — г 1 .
Сейчас…
Я хочу, чтобы вы смотрели на меня, и я хочу, чтобы вы слушали меня.
Мы собираемся войти в совершенно новый мир сумасшествия, и я собираюсь сказать кое-что нехорошее. Вы готовы?
Так г 1 это 3 ↑↑↑↑ 3, иначе НЕТ Я ДАЖЕ НЕ МОГУ.
Следующим шагом нам нужно добраться до g 2 . Вот как мы туда доберемся:
Внимательно посмотрите на этот рисунок, пока не поймете, насколько он нехорош.Тогда продолжим.
Так что да. Мы провели весь день , продирая путь от одной стрелы к четырем, преодолевая трудности, которые представлял нам каждый новый уровень операции, впитывая возмутительный эффект добавления каждой новой стрелы. Мы продвигались медленно и неуклонно, и в итоге мы в НЕТ Я ДАЖЕ НЕ МОГУ.
Затем Грэм решает, что для g 2 он просто сделает то же самое, что и для g 1 , , за исключением того, что вместо четырех стрелок будут НЕТ Я НЕ МОГУ ДАЖЕ стрелки.
Стрелки. Целый g 1 теперь подается в g 2 как его количество стрелок.
Простой переход к пятой стрелке заставил бы меня взорваться, но количество стрелок в g 2 не пять — это намного, намного больше , чем количество планковских объемов, которые могли бы поместиться во Вселенной , далеко, намного больше , чем гуголплекс, и намного, намного больше , чем БЕЗУМИЕ. И это количество стрел. Это уровень операции г 2 использования. Число Грэма повторяет концепцию итераций. Он связывает саму последовательность гиперопераций .
Конечно, мы даже не будем делать вид, что делаем что-либо с этой информацией, кроме как смеяться над ней, смотреть на нее и возбуждаться от нее. Мы ничего не можем сказать о g 2 , поэтому не будем.
А как насчет g 3 ?
Как вы уже догадались, если умножить смехотворное g 2 , получится число стрел в g 3 .
И снова это происходит для g 4 . И снова для g 5 . И снова, и снова, и снова, вплоть до g 64 .
И снова для g 5 . И снова, и снова, и снова, вплоть до g 64 .
г 64 — это число Грэма.
Все вместе это выглядит так:
Ну вот. Новая вещь, о которой снятся кошмары.
________
П.С. Написание этого поста сделало меня гораздо менее склонным выбирать «бесконечность» в качестве ответа на вопрос об обеденном столе на этой неделе.Представьте, что вы прожили года по числу Грэма. 8 Даже если гипотетически условия во Вселенной, в Солнечной системе и на Земле навсегда останутся неизменными, человеческий мозг никак не устроен так, чтобы выдерживать такие промежутки времени. Я с ужасом думаю об этом. Я думаю, что вбить бесконечность в калькулятор было бы величайшей из серьезных ошибок — и это от человека, который открыто боится смерти. Как ни странно, мысли о числе Грэма на самом деле заставили меня немного спокойнее относиться к смерти, потому что это напоминание о том, что я на самом деле не хочу жить вечно — я действительно хочу умереть в какой-то момент, потому что оставаясь в сознании для вечность еще страшнее. Да, смерть приходит, так слишком быстро, но мысль «я действительно хочу умереть в какой-то момент» является для меня очень новой концепцией и на самом деле делает меня более расслабленным, чем обычно, в отношении нашей смертности.
Да, смерть приходит, так слишком быстро, но мысль «я действительно хочу умереть в какой-то момент» является для меня очень новой концепцией и на самом деле делает меня более расслабленным, чем обычно, в отношении нашей смертности.
P.P.S. Если нужно, еще один пост «Подождите, но почему» с большими числами.
Если вам это понравилось, возможно, вам также понравится:
Размещение 7,3 миллиарда человек в одном здании
Что делает тебя тобой?
Что можно купить на 241 триллион долларов?
______
Если вам нравится «Подождите, но почему», подпишитесь на рассылку «Подождите, но почему» , и мы будем присылать вам новые сообщения сразу после их выхода.
Если вы хотите поддержать Wait But Why, вот наш Patreon .
Калькуляторкубических ярдов
Вычисление площади прямоугольника
Использование калькулятора
Рассчитать объем в кубических ярдах для ландшафтного материала, мульчи, наполнителя, гравия, цемента или контейнеров. Введите размеры в единицах измерения США (дюймы или футы) или метрических единицах (сантиметры или метры), чтобы рассчитать кубические ярды, кубические футы и кубические метры.Также рассчитать стоимость материалов, когда вы вводите цену за кубический фут, цену за кубический ярд или цену за кубический метр.
Введите размеры в единицах измерения США (дюймы или футы) или метрических единицах (сантиметры или метры), чтобы рассчитать кубические ярды, кубические футы и кубические метры.Также рассчитать стоимость материалов, когда вы вводите цену за кубический фут, цену за кубический ярд или цену за кубический метр.
Введите измерения в единицах США или метрических единицах. Рассчитайте объем на основе ваших измерений в дюймах (дюймах), футах (футах), ярдах (ярдах), сантиметрах (см) или метрах (м). Вы также можете ввести десятичные значения. Например, если у вас есть одно измерение, которое составляет 7 футов 3 дюйма, вы можете ввести его как 7,25 фута (3 дюйма/12 дюймов = 0,25 фута). Если у вас есть измерение 245 см, вы также можете ввести его как 2.45 м.
Если у вас есть площадь в квадратных футах, вы все равно можете вычислить кубические ярды. В калькуляторе выберите Прямоугольник. Введите квадратные футы в поле «Длина» и введите «1» в поле «Ширина».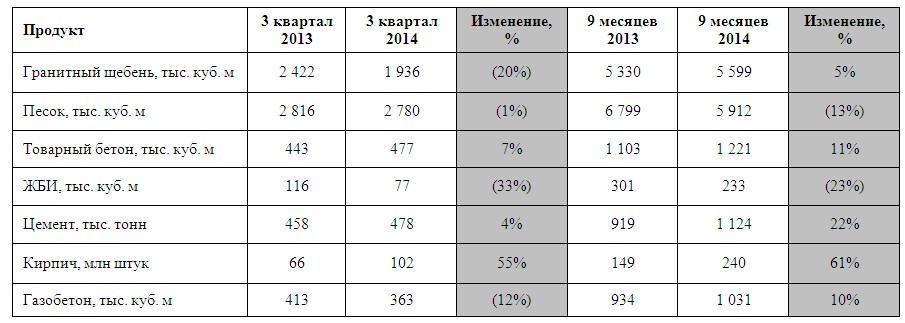 Введите глубину заливки в поле «Глубина». Нажмите «Рассчитать», и ваш ответ будет показан в кубических ярдах.
Введите глубину заливки в поле «Глубина». Нажмите «Рассчитать», и ваш ответ будет показан в кубических ярдах.
Как рассчитать кубические ярды, используя футы и дюймы
Мера
- Измерьте площадь в футах
- Определите толщину вашего материала, скажем, мульчи, которую вы уложите на эту область, используя толщину в дюймах
Переведите все измерения в футы
- Если вы измеряли только в футах, перейдите к пункту «Рассчитать»
- Если вы измеряли в футах и дюймах, разделите дюймы на 12 и прибавьте это к измерению в футах, чтобы получить общее количество футов
- Если вы измеряли только в дюймах, разделите дюймы на 12, и это будет ваше измерение в футах
Расчет кубических ярдов
- Рассчитайте площадь
- Рассчитайте объем: умножьте площадь на глубину, чтобы получить объем в кубических футах
- Подсчитайте свои кубические ярды: разделите кубические футы на 27, чтобы преобразовать в кубические ярды, и это ваш ответ
- Где ft 2 = квадратный фут, ft 3 = кубический фут, ярд 3 = кубический ярд
Кубические ярды Формулы и расчет площади
Площадь Площадь
Рассчитать кубические ярды, используя глубину в квадратная площадь
Используя измерения в футах:
Площадь, м 2 = 2 x длина стороны
Объем, футы 3 = Глубина x Площадь
Объем в кубических ярдах 3 = Объем в футах 3 / 27
Площадь прямоугольника
Рассчитать кубические ярды, используя глубину в площадь прямоугольника
Используя измерения в футах:
Площадь, м 2 = длина x ширина
Объем, футы 3 = Глубина x Площадь
Объем в кубических ярдах 3 = Объем в футах 3 / 27
Область границы прямоугольника
Рассчитать кубические ярды, используя глубину в область границы прямоугольника
Используя измерения в футах:
Внутренняя площадь (футы 2 ) = длина x ширина
Общая площадь (футы 2 ) = (Длина + (2 x Ширина границы)) x (Ширина + (2 x Ширина границы))
Площадь (футы 2 ) = Общая площадь — Внутренняя площадь
Объем (футы 3 ) = Глубина x Площадь
Объем в кубических ярдах (ярды 3 ) = Объем (футы 3 ) / 27
Площадь круга
Рассчитать кубические ярды, используя глубину в площадь круга
Используя измерения в футах:
Площадь (футы 2 ) = Pi x (диаметр/2) 2
Объем (футы 3 ) = глубина x площадь
Объем в кубических ярдах (ярды 3 ) = Объем (футы 3 ) / 27
Пи = 3. 14
14
Окружная граница
Рассчитать кубические ярды, используя глубину в область границы круга
Используя измерения в футах:
Внешний диаметр = внутренний диаметр + (2 x ширина границы)
Внешняя территория (футы 2 )
= Pi x (внешний диаметр/2) 2
Внутренняя площадь (футы 2 )
= Pi x (внутренний диаметр/2) 2
Площадь (футы 2 ) = Внешняя площадь — Внутренняя площадь
Объем (футы 3 ) = Глубина x Площадь
Объем в кубических ярдах (ярды 3 ) = Объем (футы 3 ) / 27
Пи = 3. 14
14
Очевидно, что Граница Круга и Кольцо одинаковы, только измеряются по-разному.
Площадь кольцевого пространства
Рассчитать кубические ярды, используя глубину в площадь кольца
Используя измерения в футах:
Внешняя зона (футы 2 )
= Pi x (внешний диаметр/2) 2
Внутренняя площадь (футы 2 )
= Pi x (внутренний диаметр/2) 2
Площадь (футы 2 ) = Внешняя площадь — Внутренняя площадь
Объем (футы 3 ) = Глубина x Площадь
Объем в кубических ярдах (ярды 3 ) = Объем (футы 3 ) / 27
Пи = 3. 14
14
Очевидно, что Граница Круга и Кольцо одинаковы, только измеряются по-разному.
Площадь треугольника
Рассчитать кубические ярды, используя глубину в площадь треугольника
Используя измерения в футах:
Площадь (футы 2 ) = (1/4) x квадратный корень [ (a+b+c) x (b+c-a) x (c+a-b) x (a+b-c) ]
Объем (футы 3 ) = Глубина x Площадь
Объем в кубических ярдах (ярды 3 ) = Объем (футы 3 ) / 27
Площадь трапеции
Рассчитать кубические ярды, используя глубину в площадь трапеции
Используя измерения в футах:
Площадь (футы 2 ) = ((a + b) / 2 )h
Объем (футы 3 ) = Глубина x Площадь
Объем в кубических ярдах (ярды 3 ) = Объем (футы 3 ) / 27
Как рассчитать объем бетона для лестницы
Как рассчитать объем бетона для лестницы:
Лестница – одна из неотъемлемых частей здания. Это помогает людям получить доступ к различным этажам в здании. В этой статье я объясню, как рассчитать объем бетона и количество цемента, песка, заполнителей для лестницы. Прежде чем начать оценку, нам нужно знать различные компоненты лестницы, которые я буду использовать в этом расчете.
Это помогает людям получить доступ к различным этажам в здании. В этой статье я объясню, как рассчитать объем бетона и количество цемента, песка, заполнителей для лестницы. Прежде чем начать оценку, нам нужно знать различные компоненты лестницы, которые я буду использовать в этом расчете.
Компоненты лестницы:
шагов:
Часть лестницы, состоящая из проступи и подступенка, обеспечивающая подъем и спуск с одного этажа на другой.
Протектор:
Горизонтальная верхняя часть ступени, на которую ставится нога при подъеме или спуске по лестнице.
Подступенок:
Вертикальная часть ступени, поддерживающая ступени.
Рейс:
Серия шагов без какой-либо платформы, перерыва или приземления в их направлении.
Посадка:
Платформа или место для отдыха между двумя маршами.
Теперь перейдем к расчету объема бетона для лестницы.
Возьмем пример:
Высота одного этажа = 12 футов.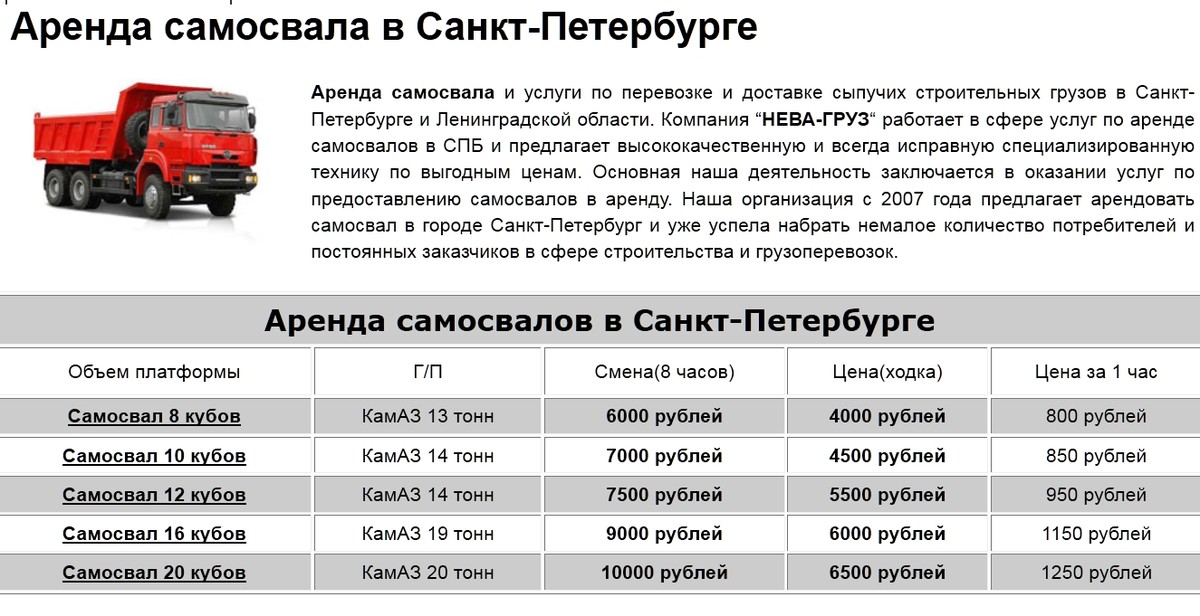
Высота, набираемая за один пролет = 12/2 = 6 футов.
Подступенки = 6 дюймов = 0,5 фута.
Количество свободных концов = высота пролета / свободный конец = 6/0,5 = 12
Протектор = 10″ = 0,8 фута.
Количество ступеней = (Количество подступенков -1) = 12 – 1
Толщина поясной плиты = 6 дюймов = 0,5 фута
Длина шага = 5 футов
Объем бетона для ступеней:
Объем одной ступени = 1/2 х подступенок х проступь х длина ступени
= 1/2 х 0,5 х 0,8 х 5 = 1,03 = 1 кубический фут.
Поскольку у нас есть 11 ступеней в марше, объем ступеней для первого марша = 11 x 1 = 11 кубических футов.
Объем бетона для поясной плиты:
Для расчета объема бетона для поясной плиты нам необходимо знать наклонную длину поясной плиты.
Горизонтальная длина поясной плиты = Проступь x Количество ступеней
= 0,8333′ x 11 = 9,2 фута.
Высота верхней площадки от пола = количество подступенков x высота подступенка
= 12 х 0,5 = 6 футов.
Объем бетона для поясной плиты = наклонная длина поясной плиты x ширина поясной плиты x толщина поясной плиты
= 11′ х 5′ х 0.5′
= 27,5 кубических футов
∴ Объем бетона для первого марша = Объем поясной плиты + Объем ступеней
= 27,5+11 = 38,5 кубических футов
Объем бетона для площадки лестницы:
Длина площадки = 10,5 футов
Ширина площадки = 5 футов
Толщина посадки = 0,5 фута
∴ Объем бетона для площадки = 10,5 футов x 5 футов x 0,5 футов = 26 кубических футов.
Объем бетона для 2-го марша лестницы:
Так как 1-й свет и 2-й марш в нашей лестнице одинаковы, то и объем бетона будет одинаковым.
Объем бетона для 2-го марша лестницы = 38,5 кубических футов.
∴ Общий объем бетона для лестницы = Объем первого марша + Объем второго марша + Объем площадки
= 38,5 + 38,5 + 26
= 103 кубических фута.
Ну, это влажный объем бетона. Чтобы преобразовать влажный объем в сухой, нам нужно умножить
на 1,54.∴ Сухой объем бетона = 103 x 1,54 = 159 кубических футов.
Количество материалов для лестницы:
Рассчитаем для Бетонной смеси 1:2:4.
1. Объем цемента = 1/7 x Сухой объем = 1/7 x 159 = 22,66 кубических футов.
∴ Количество мешков с цементом = объем цемента / объем мешка с цементом = 22,66 / 1,25 = 18 номеров мешков. (Объем одного мешка цемента 50 кг = 1,25 куб.фута)
2. Объем песка = 2/7 x Сухой объем = 2/7 x 159 = 45 кубических футов.
3. Объем заполнителя = 4/7 x Сухой объем = 4/7 x 159 = 91 кубический фут.
Примечание: Здесь я использовал кубические футы и соотношение смеси 1:2:4, вы можете использовать кубический метр и любое другое соотношение смеси бетона.
Читайте также —
Как рассчитать количество цемента, песка, заполнителей для строительства.

 Остальное будет поровым пространством. Иными словами, пористость песка будет 40%
Остальное будет поровым пространством. Иными словами, пористость песка будет 40%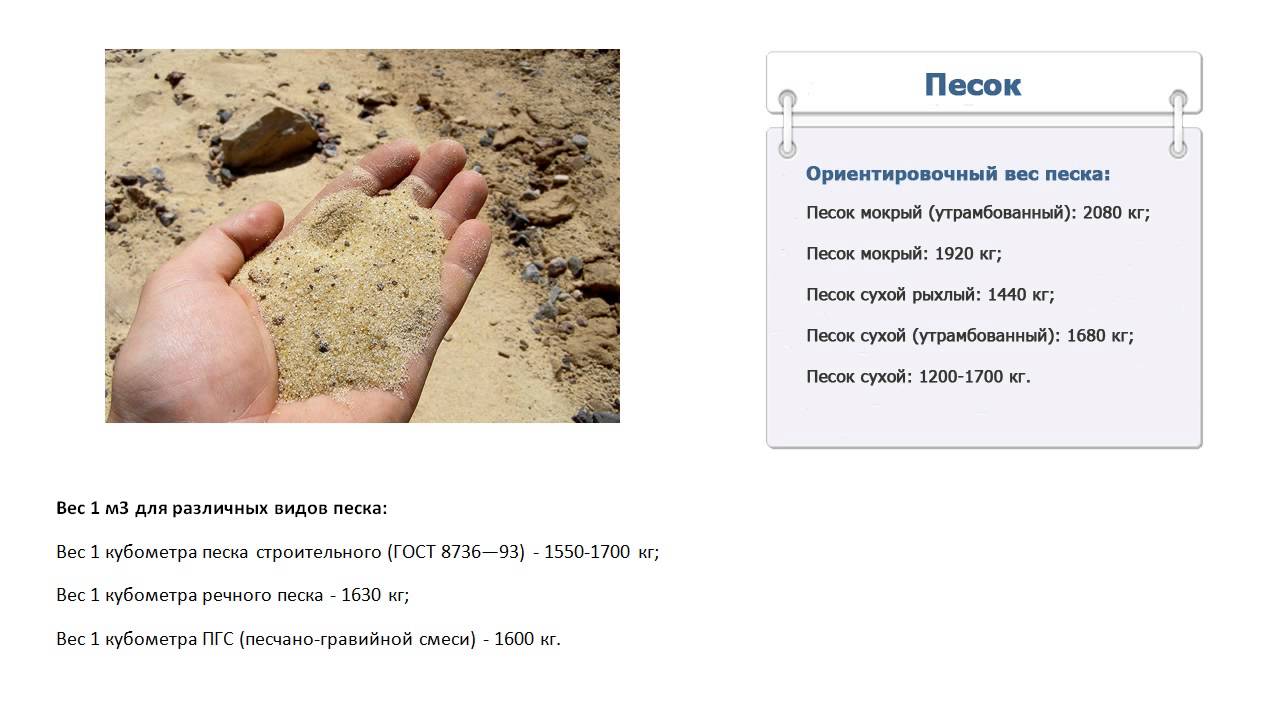 Каждый из них мог бы вместить одно сферическое зерно, если бы они были сложены друг над другом.
Каждый из них мог бы вместить одно сферическое зерно, если бы они были сложены друг над другом.